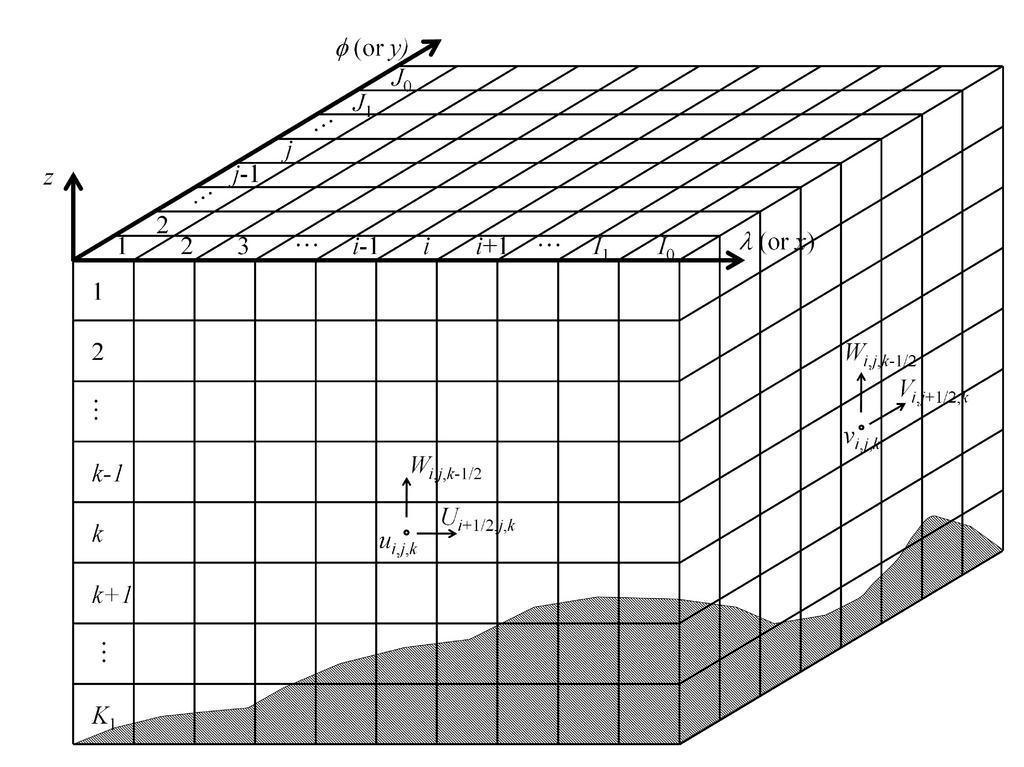
Figure N.1: computational grids in TIMCOM.
Numerical Methods
TIMCOM is an efficient and accurate model using the second-order Leap-frog temporal scheme with fourth-order spatial approximation. Furthermore, the modified Robert-Asselin filter is employed to eliminate the time splitting issue. The model domain is discretized by a set of resolution parameters, i.e. I0, J0, and K0 along the horizontal and vertical directions with the grid index i, j, and k, respectively. A non-uniform grid spacing can be set (the non-uniform vertical layers). For variable arrangement, TIMCOM uses a blend of collocated and staggered grids structures (Arakawa A and C grids). The cell-averaged variables ui,j,k, vi,j,k, Si,j,k, Ti,j,k, pi,j,k, and ρi,j,k are defined at the cell center (i, j, k), while the face-averaged velocity components Ui+1/2,j,k, Vi,j+1/2,k, and Wi,j,k+1/2 are located on the faces (i+1/2, j, k), (i, j+1/2, k), and (i, j, k+1/2). Note that ρi,j,k in the model represents density variations ρ′, which is a small deviation from the mean reference value ρ0, i.e. ρ′=ρ−ρ0. As a consequence, pi,j,k indicates pressure perturbations, rather than the total pressures.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|